Fisher's Exact Test

Fisher's Exact Test

This appendix documents Fisher's Exact Test (FET) calculation methods and presents staff's comparison of Z-test and FET results.

Calculation methods

Calculation methods and examples for percentage measures where lower values represent better performance are presented in Attachment 1. Calculation methods and examples for percentage measures where higher values represent better performance are presented in Attachment 2.

Convergence of Z-test and FET results

Staff compared Type I error values (alpha probabilities) produced by the Z-test with those produced by the FET for one "lower is better" submeasure and one "higher is better" submeasure. Staff found that the results from the two tests converge for large sample sizes. Specifically, the size of the difference between the alphas calculated for each test was highly negatively correlated with the natural log of the CLEC sample size as listed in Table 1. "Highly negatively correlated" means that as sample size increases, the difference between the Z-test alpha and the FET alpha decreases in a close and predictable relationship.

Table 1

	Measure type	Sample sizes	N	Correlation coefficient	p
	High is better	1 to 100	102	-0.89	0.00
	High is better	All	204	-0.74	0.00
	Low is better	All	167	-0.94	0.00

The correlation for the whole sample for the "high is better" measure is artifactually smaller than for the half-sample because the difference between the alphas for the two tests reduced to zero and could not diminish further for very large sample sizes. Thus though the convergence was perfect for very large samples, since there was no variation, the correlation was zero for this part of the bivariate distribution.

Table 2 lists the extent of the differences between the alphas for the two tests and illustrates the convergence of the results as sample sizes increase.

Table 2

	Measure type	Sample sizes	N	Mean difference	Median difference
	High is better	1 to 30	63	0.12	0.09
		31 to 100	39	0.009	0.00
		101 +	102	0.0006	0.00
	Low is better	1 to 100	102	0.40	0.44
		101 to 500	27	0.12	0.11
		501 to 1500	21	0.05	0.06
		1500 +	17	0.015	0.02

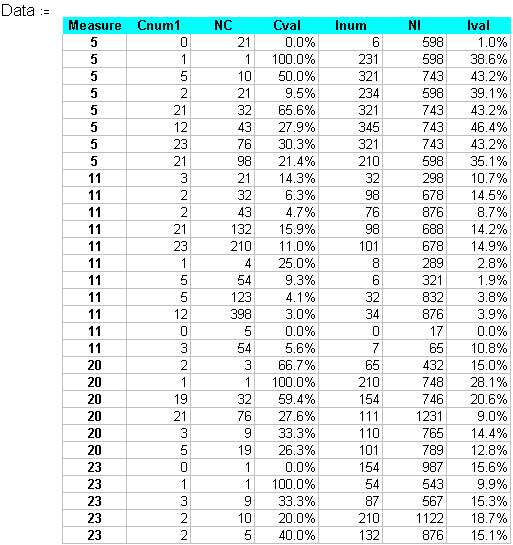
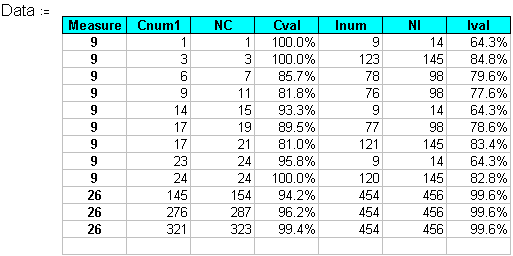
Mathcad worksheet: Hypothetical data example calculations for Fisher's Exact test. Measures for which low values represent good service.

Data :=

Numerator for CLEC

Denominator (sample size) for CLEC

Numerator for ILEC

Denominator for ILEC

The following function calculates Fisher's exact test using the above four parameters. If the CLEC numerator (HC) is zero, the probability is 1 regardless of the other parameters

.

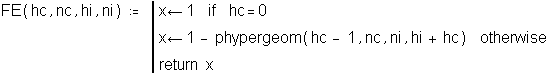
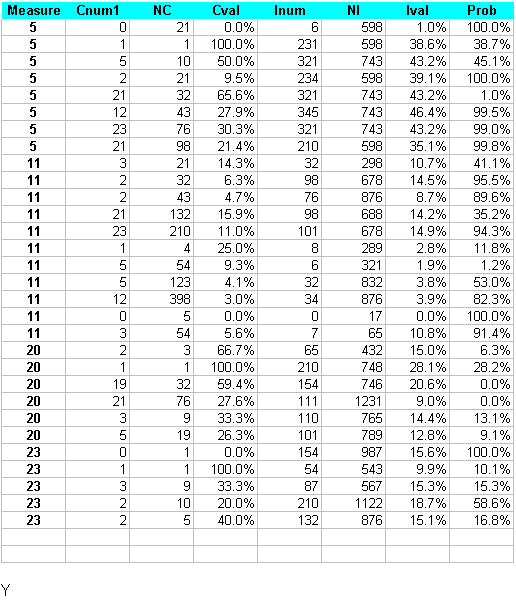
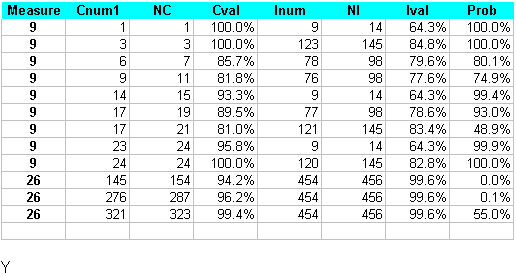
Mathcad worksheet: Hypothetical data example calculations for Fisher's Exact test. Measures for which high values represent good service.

Data :=

Numerator for CLEC. This value is

converted from "hits" to "misses".

Denominator (sample size) for CLEC

Numerator for ILEC, also converted

from "hits" to "misses."

Denominator for ILEC

The following function calculates Fisher's exact test using the above four parameters. If the CLEC numerator (HC) is zero, the probability is 1 regardless of the other parameters.
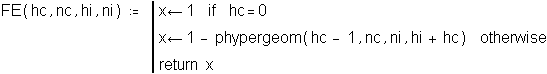