Balancing Alpha and Beta Error

Balancing Alpha and Beta Error

This appendix documents staff's efforts to balance alpha and beta error levels for performance result assessment. To calculate the "balance point" for alpha and beta error staff adapted a balancing formula presented in Das (1994). Staff treated this formula as a "equal error" formula by assuming equal consequences for the two types of error. The formula was also adapted by including the "N" for both ILEC and CLEC samples. The formula as used was:

Z_{_} = ((H₀-H_alt)/SD_i*sqrt(1/N_c+1/N_i))/2

Where:

H₀ = Null hypothesis (ILEC mean)

H_alt = Alternate hypothesis

SD_I = ILEC standard deviation

N_c = CLEC sample size

N_I = ILEC sample size

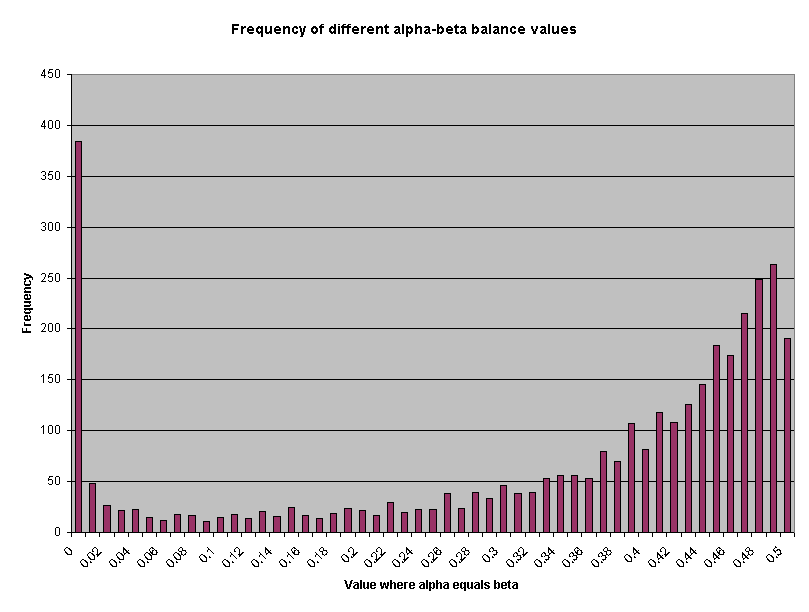
Staff analyzed Pacific's May, 2000, performance results to estimate the effects of setting critical alpha levels equal to beta error for each result. An alternate hypothesis of 50-percent worse performance was assumed for the calculations. In other words, staff estimated the critical alpha level that would result in equal error (beta) in detecting performance at least 50% worse for the CLEC as for the ILEC. On the average, alpha balanced with beta at a value of 0.33. In other words, if alpha error was held to a maximum of 33 percent, beta error would also be 33 percent. Table 1 presents the summary statistics.

Table 1

	Alpha balanced with beta
	N		3481
	Mean		0.33
	Median		0.41
	Minimum		0
	Maximum		0.5

Attachment 1 presents a frequency distribution of the balancing values.

Staff also calculated the resulting error rates with an alpha error rate "ceiling." Table 2 presents summary statistics for those calculations.

Table 2

	Critical alpha levels resulting from different alpha/beta balance limits
				Alpha limit
			0.33	0.25	0.2
	N		1204	894	782
	Mean		0.131	0.0726	0.0499
	Median		0.11	0.02	0.01
	Mode		0	0	0
	Minimum		0	0	0
	Maximum		0.33	0.25	0.2

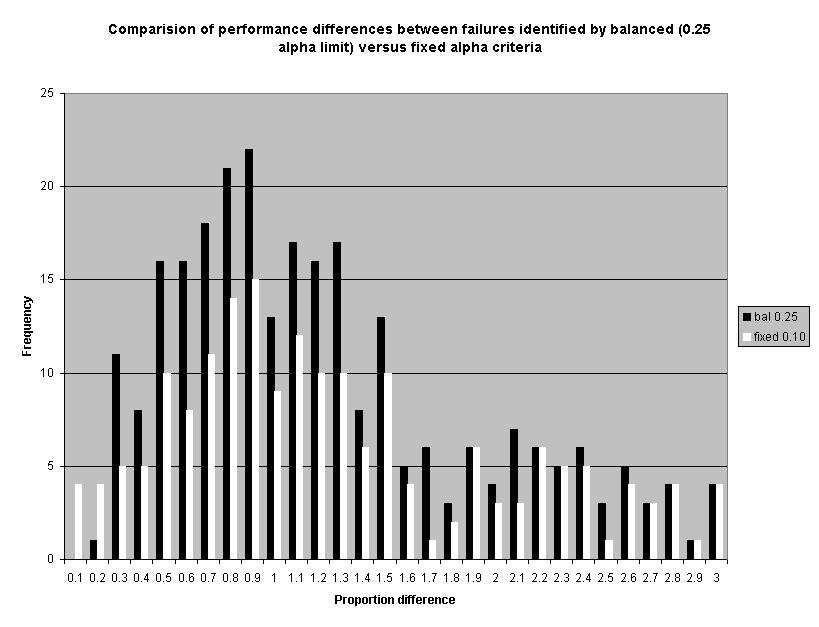
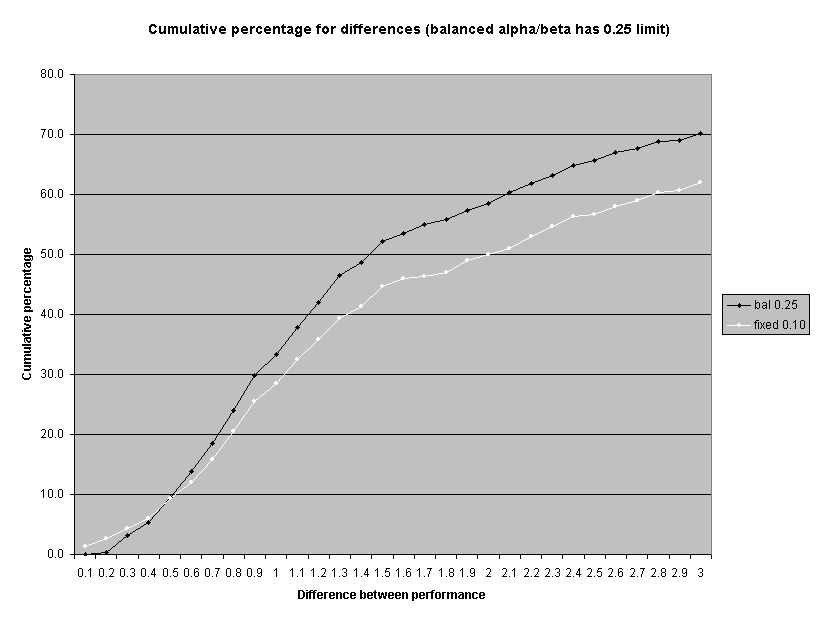
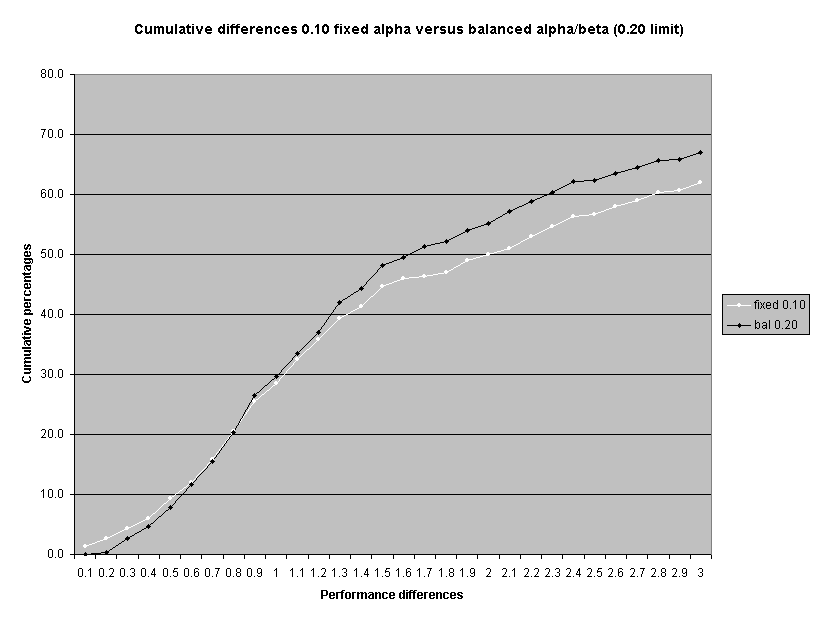
Staff also examined the net effect on the size of the difference between ILEC and CLEC performance that would be identified as a performance failure. Theoretically, balancing alpha and beta should result in an increase in larger differences being detected and a decrease in smaller differences being detected. Attachment 2 shows that this in fact would occur. Limiting alpha to 0.25, for example, results in a lower proportion of failure identifications where performance to a CLEC is zero to 50 percent worse than ILEC performance to itself (Attachment 2, page 2), relative to a fixed 0.10 alpha criterion. Conversely, this limit results in a greater proportion of failure identifications where performance to a CLEC is at least 50 percent worse than ILEC performance to itself. These charts only display results up to the point where performance to a CLEC is three times worse than performance for the ILEC. At this point, however, there are no further differences between a fixed 0.10 alpha criterion and either the 0.20 or 0.25 alpha/beta balance limited criteria.